Causal Set Theory
What are causal sets and how are they quantum gravity?
Causal Set Theory is an approach to quantum gravity that postulates that spacetime is fundamentally discrete — it takes the form of a causal set, whose elements are the indivisible ‘‘atoms’’ of spacetime. These atoms are ordered so that the past of an element corresponds to all the elements which precede it. In this way, a causal set gives a causal structure — a notion of before and after — in the absence of a continuum.
Causal Sets
What do we need to know in order to defined a spacetime? In fact, we can reconstruct all the mathematical structure of spacetime geometry (topology, differential structure and metric) up to a conformal factor just from its causal structure. The only thing causality does not provide is scale, leaving us with a family of conformally related geometries that are only fixed when we somehow give it a spacetime volume.
What if we introduce a natural cutoff that is inherent to the theory? A minimum length in spacetime at around Planck scale (problems usually start to emerge) would make spacetime discrete instead of a continuum. This means we are unable of moving an infinitesimal distance, but only distances above this minimum length and multiples of it. We can picture these as spacetime atoms.
What if we introduce a natural cutoff that is inherent to the theory? A minimum length in spacetime at around Planck scale (problems usually start to emerge) would make spacetime discrete instead of a continuum. This means we are unable of moving an infinitesimal distance, but only distances above this minimum length and multiples of it. We can picture these as spacetime atoms.
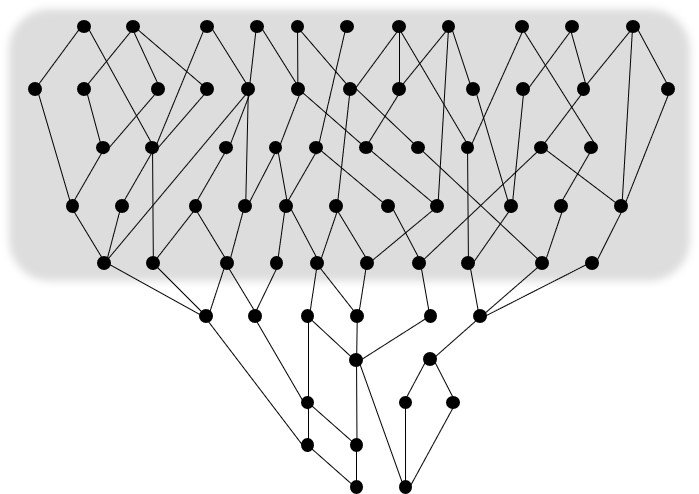
We then get a discrete manifold, with a particularly interesting property: we can get scale just by counting. If we take spacetime to be discrete, causal structure alone is enough to fully reconstruct its geometry. This is the basis of the Causal Set Hypothesis.
Causal Set Hypothesis: The underlying structure of spacetime is discrete and its elements are equipped with a causal structure that fully determines its geometry. The spacetime continuum is a coarse-grained approximation of a Causal Set.